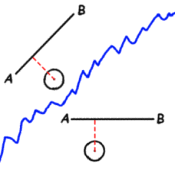These tutorials try to solve basic problems using easy to understand solutions rather than optimized complex math. Basically, this is a simple way of getting to the answer, not an elegant collection of mathematical skill.

The first goal is to find the closest line to the circle using whatever method is best for the environment the objects are in. When the initial search to find the nearest line is complete, use point A as the base point and rotate the line AB so that B is 0 degrees from A. The circle position is also rotated to maintain local calculations.

Once this is done, the collision point will be the x coordinate of the circle and the y coordinate of line AB. Next find the distance from the center of the circle to the collision point. If this distance is less than the radius of the circle then a collision has occurred.

Now that the collision point is found, how is the circle supposed to react? There are two main collision possibilities - one where the circle hits the line straight on and one where the end of the line hits the circle (assuming there is no adjacent line).

For the first case, all that is needed is to take the current angle of the circle and rotate the value to correspond to the rotation amount for the line AB (the initial rotation we did). Therefore, the new angle for the circle direction is 360 - new circle direction with 360 being a full circle rotation and new circle direction being the direction of the circle after rotating it to correspond to the AB rotation change.

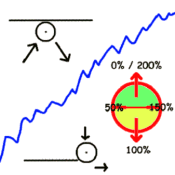After completing this calculation, rotate the circle in the reverse direction of the initial AB line rotation to preserve global values. For example, assuming the line is already rotated, suppose the circle is going at a 45 degree angle as in the diagram. Using the calculation above, the new direction should be in the area of 360 - 45 = 315°.

In the second case, because the collision point is automatically the endpoint, the first step of rotating the line and circle is not required. When the circle hits a line at a point which does not correspond to the direction the circle is heading will indicate that the circle was hit from the side. This tutorial assumes that the line is part of an object which is not actually moving, thereby we will not have to account for any momentum changes.

As per the diagram in the second image, if the circle is hit anywhere on the green area it must be moving upwards and conversely the same is true for the yellow area. As well, to make sure our following calculations are correct, we will use the example indicated in the second image. If the circle is moving at 270° and the circle is hit at 225° then the resulting direction should be 0°. We will check this later on.

There are two ways of calculating the resulting direction. The first is straight forward and easier to understand whereas the second (upon rewriting this tutorial) seems somewhat muddy but is included for the sake of completeness.

By calculating x1 = 360 - (impact direction - circle direction) and following that with the calculation x2 = (x1 * 2) + 180, the new direction of the circle is circle direction - x2. Using the example stated above - we get x1 = 360 - (225 - 270) = 405° which then leads to x2 = (405 * 2) + 180 = 990° = 270° and finally 270 - 270 = 0°.

Now for the second way of calculating an endpoint collision. If the circle direction is changed to equal 90°, we can use the colored circle in the second image. If we calculate the strength of impact using the equation x1 = (impact direction / 90) * 100 we get a value which will correspond to the diagram (where 90 = 1/4th of a circle). From this, we add 50% so that it will correspond properly to the given angles and then convert it to an angular form using (x1 + 50) * (360 / 200). After all this remember to readjust the value to account for whatever the direction of the circle was change by to have it equal 90°.

Using the same example as before, we change the direction of the circle from 270° to 90°, thereby also changing the angle of impact from 225° to 45° since we need to subtract 180°. We then get x1 = (45 / 90) * 100 = 50°. Now we calculate the resulting direction getting (50 + 50) * (360 / 200) = 180°. Finally, we have to counter rotate by 180° because of the original rotation (to get 90°) for a value of 180 + 180 = 360° = 0°.

This ends the tutorial. As indicated in the beginning, this tutorial is only to give an idea of how to get things going and because of that some cases and/or calculations may be missing or just skipped to simplify things. If anyone has any comments or questions, please feel free to email.