These tutorials try to solve basic problems using easy to understand solutions rather than optimized complex math. Basically, this is a simple way of getting to the answer, not an elegant collection of mathematical skill.

Tutorial #3 went over how to calculate normals and basic ideas of how collisions would be calculated. Normals themselves can be used for lighting, shadows, reflections, etc. but for what both tutorials #3 and this one, we are going to use normals to help calculate collisions. To review quickly what tutorial #3 went over, it was assumed that two points were looked at. They were time based variations of the same point and if each point were on separate sides of the polygon in question, naturally a collision would occur.

Since polygons have boundaries and are do not go on forever, we will need to allow a structure for calculating various things we want to do to our polygons. Without boundaries collisions would occur anywhere as long as the point passed through the plane and for things such as decals, we need the boundaries to calculate edges. Another reason for using boundaries with polygons is to provide pre-calculated values which will help with rendering and object interaction.

How the triangles/polygons are handled may be overkill but it allows for further growth when dealing with the triangles. The triangle structure includes float3 center, normal[4], point[3]; with float3 being a variable with 3 floats - x, y and z. In this case we have a center which helps with calculations, point[3] for the 3 points in the triangle and normal[4] which is for the main normal [0] and the 3 sides [1..3]. To calculate all the normals, all we have to do is first calculate the main normal. Once we get that value which shows the direction the plane is facing, we can normalize the value, which again sets the length to 1.

Now we can create a new triangles for the boundaries by using the base triangle and the normal to setup three other triangles:

newPoint1 = baseTrianglePoint1; newPoint2 = baseTrianglePoint2; newPoint3 = baseTrianglePoint1 + normal;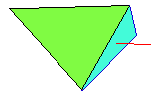

This will allow a new triangle in which we can calculate a normal for. After doing this for all three edges we end up with four normals - one for the base triangle and three more for the sides. As can be seen in the picture, the green triangle is the original, the blue triangle is the newly formed triangle and the red line is new normal. With all four normals we can then calculate if a collision occurs within the boundaries:

1 - Does collision occur with main triangle?
2 - If so, calculate the collision point.
3 - Does the collision point occur within the boundaries?
4 - If so, calculate collision.

Checking whether the collision point occurs within the boundaries is as easy as checking the sign of the dot product and going forward from there. For the boundaries themselves, it could be used as another way of partitioning a larger area as opposed to using oct-trees and portals. Instead of rendering a lot of moving objects which may be slow in those algorithms - a quick check on some basic boundaries could relieve much need processing.

Another area where our way of boundaries could come in is when calculating things like decals when deciding whether certain features may occur within the polygon itself. An example of boundaries with decals could be an explosion over a corner wall - by using the boundaries of the wall the explosion could be wrapped around by placing it both walls that make up the corner and cutting off at the boundaries of each.

This ends the tutorial. As indicated in the beginning, this tutorial is only to give an idea of how to get things going and because of that some cases and/or calculations may be missing or just skipped to simplify things. If anyone has any comments or questions, please feel free to email.